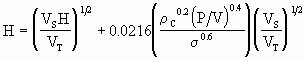Transporte de Massa na Agitação de Líquidos
Andrea Dietrich Martini, Fernando
Malta Diniz
Alunos de Pós-Graduação do Depto. de Engenharia Química da
EPUSP
Na agitação a rotação do rotor resulta em um gradiente de velocidade ao longo do tanque, causando mistura e dispersão dos componentes. A aplicação do balanço de massa dentro de um tanque agitado é muito complexa. Em primeiro lugar, o fluxo é tridimensional e as condições iniciais e de camada limite, na maioria das vezes, não são conhecidas. Geralmente, as transferências de calor, massa e momento devem ser consideradas simultaneamente. No caso de agitação de líquidos de baixa viscosidade, o fluxo é altamente turbulento, permitindo uma maior transferência. A agitação pode promover o aumento da taxa de transferência de massa quando a mistura é um soluto miscível em um solvente líquido. Se o soluto consistir de cristais sólidos, então a agitação é responsável por produzir e manter o máximo de "driving force" de concentração possível , entre a interface do sólido e a solução. O soluto pode ser um líquido ou um gás. Para o transporte de massa convectivo pode ser escrita a seguinte expressão:
onde NA é o fluxo molar da substância A, S é a área da superfície por onde se dá o transporte de massa, CAS é a concentração de A na superfície, CA¥ é a concentração de A longe da superfície e k é o coeficiente de transporte de massa. A principal dificuldade nos cálculos de transporte de massa consiste em determinar o valor de k, com as metodologias para a sua determinação variando conforme a geometria do sistema e o estado de agregação das fases entre as quais ocorre o transporte de massa, sendo o mais usual a utilização de equações adimensionais, como as apresentadas a seguir. Em todos os problemas abordados nesta seção, será considerado o transporte de massa a partir de uma esfera, em torno da qual escoa um fluido. Para maiores detalhes sobre transporte de massa em geral, podem ser consultados os livros BRODKEY & HERSHEY (Transport Phenomena), 1988, BIRD, STEWART & LIGHTFOOT (Transport Phenomena), 1960 ou praticamente qualquer outro livro da área. Sistemas Sólido - Líquido São sistemas onde partículas sólidas estão dispersas em um líquido agitado. Usualmente as expressões utilizadas neste tipo de sistema são da seguinte forma:
onde os valores de c, p e q são constantes para cada tipo de sistema. Ou seja, os valores dessas constantes dependem do tipo de rotor, do número de chicanas, das configurações geométricas do vaso, etc.... Para vasos sem chicanas podem ser utilizadas as seguintes expressões:
Uma expressão mais geral também pode ser utilizada:
onde Esta equação é válida para (dP/D)2 > 4x10-5. Para partículas não esféricas devem ser utilizadas as seguintes relações:
onde W é a massa total da amostra e n é o número de partículas. Para vasos com chicanas, com rotores do tipo propulsor ou turbina, pode ser utilizada a expressão: , com os valores para as constantes mostrados na Tabela 1. TABELA 1: Constantes da equação 1
Sistemas Líquido - Gás São sistemas em que um gás é borbulhado através de um líquido sendo agitado. A não ser em caso de menção em contrário, as expressões serão consideradas como válidas também para sistemas Líquido - Líquido. Neste item o subscrito c refere-se à fase contínua (o líquido agitado) e o subscrito d à fase dispersa (as bolhas). Para estes sistemas, podem ser utilizadas as seguintes expressões:
Para diâmetros de partícula entre 0.6 e 2.5 mm ocorre um regime de transição. Os adimensionais são assim definidos:
O diâmetro da partícula é dado pela seguinte proporcionalidade:
Para um rotor do tipo turbina, pode ser usada a relação:
onde as constantes a e b da equação 2 estão na Tabela 2. TABELA 2: Constantes da equação 2
H é o "hold -up" ou a fração de gás que está suspenso no líquido. Pode ser calculado pela diferença de altura do nível do vaso quando o sistema está sendo borbulhado e quando não. O seu valor também pode ser determinado pela expressão:
Nomenclatura: D: diâmetro do tanque;
|
[topo]
|
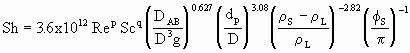 ,
,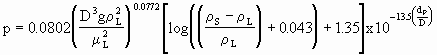
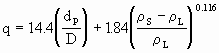
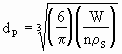 e
e 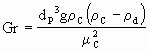 ,
, 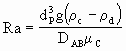
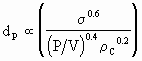
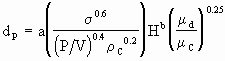 (2)
(2)