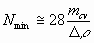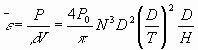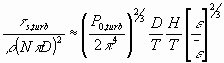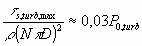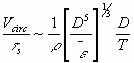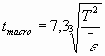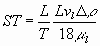Critérios de Projeto e Scale-up de Processos em cristalizadores tipo tanque agitado (STR)

O critério básico de agitação em cristalizadores é o da manutenção dos sólidos em suspensão através da menor dissipação possível de energia por volume de cristalizador. Ë recomendado o uso de chicanas para evitar a formação de vórtice e respectivo arraste de gás para o seio do líquido quando o número de Reynolds (Re) é superior a 1.000. Aqui Re é definido por:

onde:

N - rotação do rotor (s^-1);
D - Diâmetro do rotor (m)
n_{L -} viscosidade cinemática (m²/s)

Em um cristalizador tipo STR a agitação deve no mínimo garantir que os sólidos estejam em suspensão, A velocidade mínima de suspensão (N_min) é dada por

onde a velocidade volumétrica de produção de massa de um cristalizador (m_cv) é dada pela razão entre a massa gerada na unidade de tempo Mc e o seu volume V. e Dr a diferença de densidade entre o sólido e a solução.

Por razões práticas, é necessário que seja dada especial atenção ao fluxo em um cristalizador tipo STR em relação aos processos de mistura, suspensão, abrasão e aglomeração dos cristais, a destruição dos aglomerados, o transporte de massa entre os cristais e a solução e o transporte de calor entre a suspensão e a superfície de troca.

• Fluxo e tensão de cisalhamento

O fluxo volumétrico (Q_circ) no cristalizador é dado por:

sendo Q_v a capacidade de bombeamento

O fluxo volumétrico específico, , por:

onde V é o volume do cristalizador .

Para uma dada rotação, N , rotores que favorecem a movimentação de líquidos, como ,por exemplo, "propellers", requerem muito menos energia de acionamento do que os que não favorecem o fluxo de líquido, tais como as turbinas do tipo "multiple flat blade". A potência P é dada por:

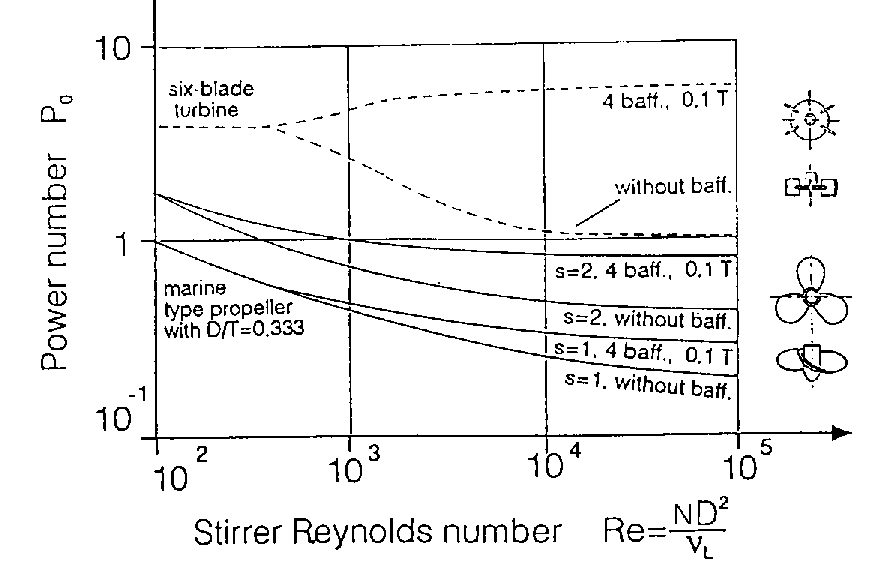
A figura 1 apresenta a capacidade de bombeamento de uma hélice marítima, com e sem chicanas e a figura 2 o número de potência (P₀) para diversos tipos de rotores.
 

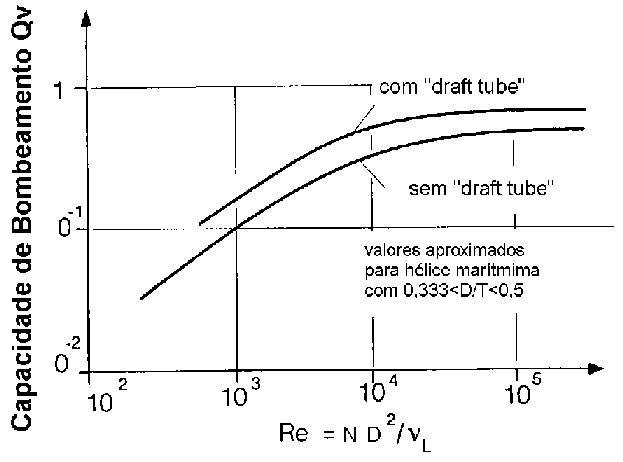
Figura 1 – Capacidade de bombeamento

 

Figura 2 – Número de Potência

Para Re>10⁴ o fluxo volumétrico, no entanto, pode ser considerado independente da configuração geométrica do cristalizador e da relação D/T. Neste tipo de cristalizador, a dissipação de energia específica média () e a local, e , diferem significativamente. A variação do valor de com a altura H do vaso agitado é dada por:

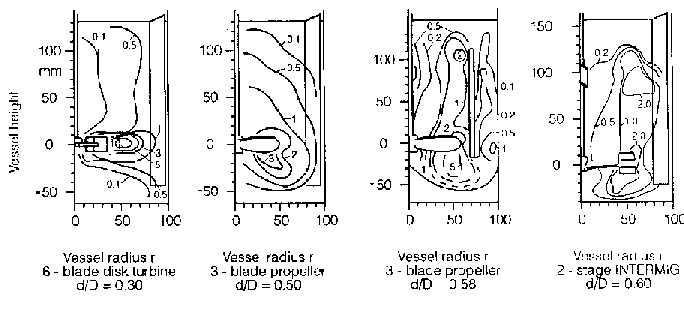
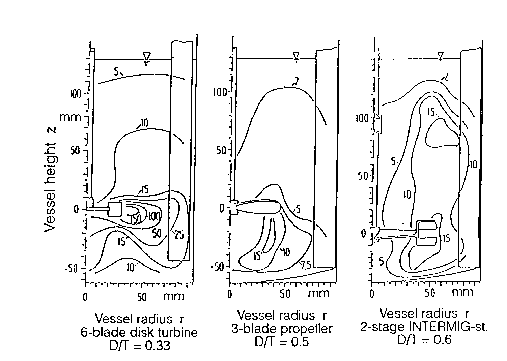
A figura 3 apresenta a variação experimental da relação entre a dissipação de energia específica local e a média. Estas linhas isoenergéticas permanecem constantes durante a ampliação de escala de cristalizadores geometricamente similares, se Re> 10⁴. Estes diagramas mostram que a região em que ocorre a maior dissipação de energia local ocorre nas vizinhanças do rotor. É neste local que ocorrerá a maior parte do atrito nos cristais maiores e nos aglomerados.

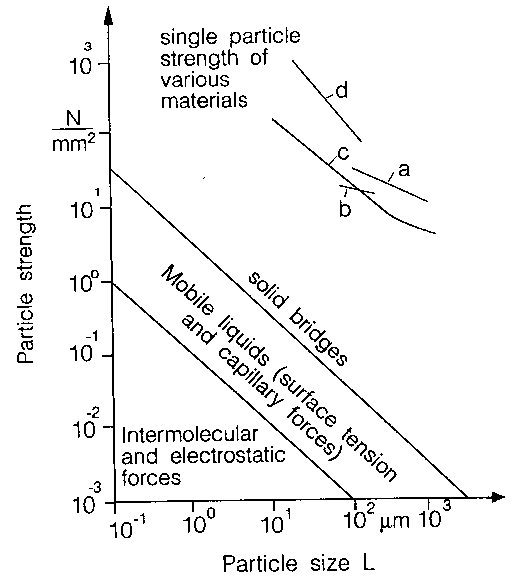
Os melhores rotores que resultam em menor atrito são aqueles cujo número de potência (P₀) é menor para uma maior capacidade de bombeamento (Q_v) e aqueles que podem ser operados com uma dissipação de energia específica média mínima relativamente à mistura e suspensão.

Aglomerados relativamente fracos podem ser destruídos por uma tensão de cisalhamento t_s. A tensão de cisalhamento teoricamente permitida para cristais e aglomerados pode ser estimada da figura 4., onde a força de tensão "tensile strenght" de aglomerados e cristais é colocada em um gráfico contra o tamanho das partículas. A tensão depende do tipo ligação entre as partículas no aglomerado: forças de capilaridade, eletrostáticas, intramoleculares ou pontes de sólidos. O aglomerado irá quebrar quando a tensão de cisalhamento do líquido t_{s ,} superar a tensão do aglomerado.

Para o regime turbulento (Re> 10⁴) a tensão de cisalhamento t_{s, turb}, pode ser estimada pela relação:

Na figura 5 apresenta-se linhas de tensões idênticas para diferentes rotores. A tensão máxima ocorre, naturalmente, também na área de saída do rotor e pode ser estimada, para diferentes tipos de rotor e com várias relações de diâmetro rotor/tanque, pela seguinte equação:

Rotores tipo hélice marítima, que favorecem o fluxo de líquido, são recomendáveis para uma circulação suave da suspensão de cristais. Quanto maior o tanque agitado e maior a relação entre o diâmetro do rotor e do tanque (D/T), a dissipação específica de energia será convertida mais em um volume de circulação específico V_circ e menos em tensão de cisalhamento média:

Esse é o motivo de se recomendar a integração da potência específica necessária para a mistura e suspensão no vaso agitado no maior rotor possível e não em vários agitadores pequenos e de se equipar cristalizadores grandes com propelidores tipo hélice marítima com D/T ³ 0,5, que favorece a circulação do líquido. Deve-se notar, no entanto, que a capacidade de mistura de cristais na suspensão diminui com o aumento do tamanho do cristalizador. Em outras palavras, uma mistura constante implicará, para a ampliação de escala, na manutenção da velocidade empregada no modelo, ou seja, de acordo com , a dissipação média de energia irá aumentar com o quadrado do diâmetro do impelidor, mantendo-se idêntica configuração geométrica. Esta grande dissipação de energia não só é antieconômica como causa uma grande quantidade de abrasão nos cristais.

• Mistura

Para Re > 10⁴, o tempo de macromistura em líquidos é dado por:

Esta relação pode fornecer valores úteis também para suspensões. O tempo de macromistura é da ordem de poucos segundos, mas pode ser consideravelmente maior na região de transição (10<Re< 10⁴), especialmente na região laminar.

A macromistura tem por objetivo compensar diferenças locais de certos parâmetros (temperatura, concentração, supersaturação, etc.), embora a relação entre o tempo de macromistura e a magnitude destas diferenças não sejam, em geral, conhecidas.

• Suspensão

O rotor deve não somente misturar os líquidos como manter os cristais suspensos. A rotação mínima, N_min, necessária para manter a suspensão de cristais pode ser determinada, considerando-se que o poder de sedimentação das partículas, P_sett , deve ser compensado pela potência do agitador, P_min , que resulte na mínima dissipação de energia, e_min = P_min/Vr_méd.

:

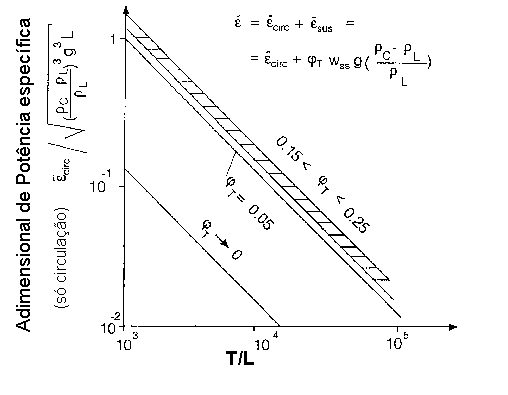
onde w_ss é a velocidade de sedimentação do sólido.

A figura 6 apresenta o adiminesional de potência específica (), como função da razão T/L para diferentes valores de fração volumétrica de sólidos, j_T , para um "propeller" com T/D = 3 em um cristalizador com H/T =1. Quando a relação entre o diâmetro do tanque (T) e o tamanho das partículas (L) é inferior a 1000 (T/L<1000), recomenda-se que o parâmetro  seja mantido constante. Para T/L >1000, o parâmetro  selecionado de modo a que a suspensão possa ter o menor valor quanto maior for o diâmetro do cristalizador em escala industrial, de acordo com a relação Np D = constante, ou . . Entretanto, deve-se notar que um fluxo volumétrico constante requer na ampliação de escala, uma rotação N constante. Infelizmente, lembrando que , mantendo-se N constante, haverá um aumento drástico na dissipação de energia , para cristalizadores geometricamente similares, implicando no aumento da nucleação secundária e, consequentemente, diminuindo o tamanho médio dos cristais.

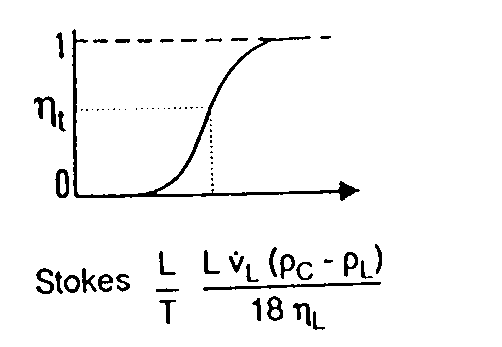
As diferentes leis que regem o processo de suspensão em vasos agitados de tamanhos variados de sólidos resultam do efeito físico de partículas colidindo (T/L® 1) ou não colidindo (T/L®¥ ) quando desviada do obstáculo (rotor, fundo do tanque, curvas), dependendo das propriedades características das partículas (diâmetro do cristal, L) e do rotor (diâmetro do rotor D) e do fluxo de entrada da suspensão. Em cristalizadores muito pequenos, a probalidade de colisão é praticamente 1 (isto é, praticamente todas as partículas colidem, resultando na formação de depósitos no fundo do tanque. Neste caso a dissipação de energia necessária permanece praticamente constante, de modo que as partículas são arrastadas do fundo para o meio líquido.

A probabilidade de colisão, h_t , (o< h_t <1) depende, acima de qualquer coisa, do número de Stokes,

como mostrado no diagrama da figura 7. Tanto na equação acima quanto na figura 7, v_l é a velocidade da partícula.

Figura 7 – Probabilidade de colisão em função do número de Stokes

[topo]