Lower Envelopes (or Coherent Lower Probabilities)

The theory of lower envelopes looks at the possibility of specifying intervals of probability for events.

First note that the existence of a convex set of distributions induces an interval of probabilities for a random variable. Given a convex set of probability distributions K, then the functions

$$\underline{p}(x) = \inf_{p \in K} p(x)$$

$$\overline{p}(x) = \sup_{p \in K} p(x)$$

are called the lower and upper envelopes of K [15,16,31].

Now it must be emphasized that there is no real agreement on the use of the word envelope. Many people refer to lower envelopes simply as ``lower probabilities.'' The problem is that the expression ``lower probability'' is also used by many to refer to structures that have a very specific axiomatization [7]; such structures are not necessarily related to sets of probabilities (Section 7). Walley uses the term coherent lower probability to refer to lower envelopes, and this seems an excellent name, but here the expression ``lower envelope'' is used to make it easier to distinguish between different concepts of coherent and incoherent lower probability.

The following fundamental conjugate relation exists between lower and upper envelopes:

$$\underline{p}(x) = 1 - \overline{p}(x^c)$$

where x^c is the complement of x. We do not need to specify both $\underline{p}$ and $\overline{p}$; $\underline{p}$ alone defines a lower envelope.

The Correspondence between Lower Envelopes and Convex Sets of Distributions

The definition above of lower envelope assumes the existence of a set of distributions. But there may be several sets of distributions that generate the same lower envelope.

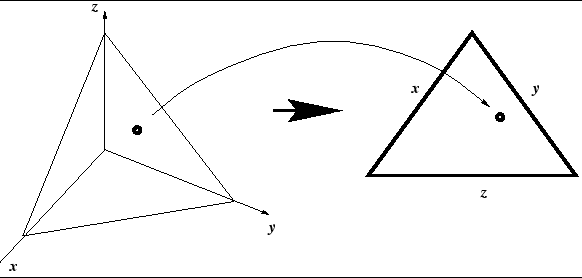
In order to emphasize this point, let us look at a construction that is very common in the language of sets of probabilities. Suppose you have an outcome space defined by three variables, x, y and z. Now, the probabilities p(x), p(y) and p(z) correspond to a 3-dimensional point with norm 1. Figure 1 shows two ways to visualize this situation. We can draw a three dimensional space and the loci of all points such that p(x) + p(y) + p(z) = 1 (a plane). Or we can draw the loci of all these points in baricentric coordinates: just a triangle, where the coordinates of a point are read as distances from that point to the sides of the triangle. It takes a while to get used to, but it is a very useful representation.

Figure 1: Cartesian and Baricentric coordinates for a probability distributions with three variables

Now look at the following picture of two convex sets of distributions in baricentric coordinates (for a three-variable type of space). The credal sets induce bounds on the probabilities for x, y and z; the lower bounds form the lower envelope. But note that the credal sets are different, despite the fact that the lower envelopes are identical.

Figure 2: Two convex sets of distributions with the same lower envelope

So now we know that there is more than a single way to specify a set of distributions inducing a given lower envelope.

The Correspondence between Lower Envelopes and Intervals of Probability

A natural question about lower envelopes is to inquire the relationship between them and intervals of probability:

Suppose you start with a system of intervals for probability. For every event you can think of, specify an interval on the real line. You don't have any particular model of probabilities at this point, just the probability intervals. Let us call the bottom of the interval for an event x by $\underline{p}(x)$.

You want to use the intervals to create a set of probability distributions. You can do that by defining the set:

$$K = \mbox{ All distributions such that } p(x) \geq \underline{p}(x), \mbox{ for all } x .$$

Now the following question becomes relevant:

If I create a interval system and then I obtain K as in the previous expression, is it possible to recover exactly the original interval system by taking the lower envelope of K? Are the intervals and the set K representing the same thing?

Note that a similar question was asked with regard to the relation between credal sets and lower expectations.

In the case of lower envelopes, the short answer to the question above is no, not in general. But a detailed answer is really more complex. We need to talk about lower probability in order to answer this question.